若狭 尊裕 Wakasa Takahiro [博士(数理学)]
総合科学教育科 助教
専門分野
- リーマンゼータ関数
- ディリクレのL関数
写真

研究課題
- リーマンゼータ関数の臨界線上の偏角およびその多重積分した関数の明示的上界
- リーマンゼータ関数の臨界線上の偏角を多重積分した関数のΩ-評価
- ディリクレのL関数の偏角およびその多重積分した関数の明示的上界
研究シーズ
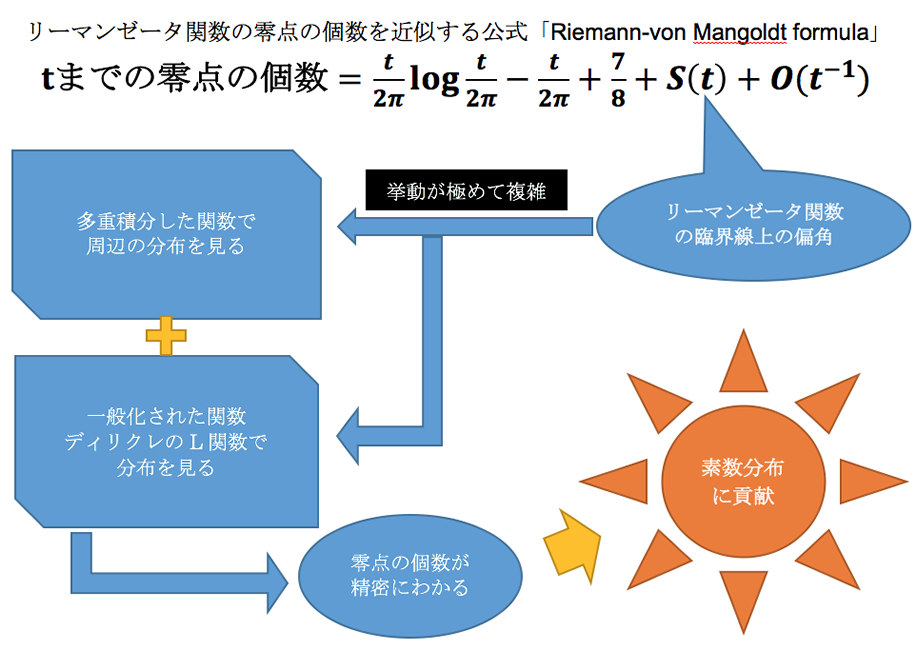
画像の解説
リーマンゼータ関数の零点の個数を近似する公式「Riemann-von Mangoldt formula」
tまでの零点の個数=t/2π log t/2π-t/2π+7/8+S(t)+O(t^(-1))
多重積分した関数で周辺の分布を見る
一般化された関数ディリクレのL関数で分布を見る
挙動が極めて複雑
零点の個数が精密にわかる
リーマンゼータ関数の臨界線上の偏角
素数分布に貢献
tまでの零点の個数=t/2π log t/2π-t/2π+7/8+S(t)+O(t^(-1))
多重積分した関数で周辺の分布を見る
一般化された関数ディリクレのL関数で分布を見る
挙動が極めて複雑
零点の個数が精密にわかる
リーマンゼータ関数の臨界線上の偏角
素数分布に貢献
研究のキーワード
リーマンゼータ関数,ディリクレのL関数












