新藤　圭介 Shindo Keisuke ［(理学博士）］

●不動点定理
　不動点とは変換によって自身に移されるような点であり、それは諸所の問題を解決するうえで重要な役割を果たす。とくに、平衡や安定性の問題は、数学や自然科学の様々な場面で登場するが、これらの概念と、不動点理論は密接な関係を持つことが知られている。したがって、不動点の存在や、不動点の見つけ方を研究することの意義は大きいと考えられる。

●測地距離空間
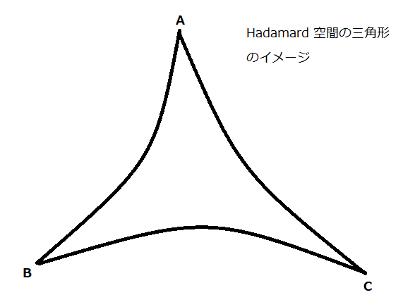
　測地距離空間は凸構造をもつ距離空間であり、凸解析学において近年盛んに研究が行われるようになった主題のひとつである。またHadamard空間は測地距離空間の代表例であり、その曲率の上限は0である。さらに、Hadamard空間はHilbert空間を一般化した概念でもあるため、この空間の性質の研究は数学的に非常に重要である。