丸岡 晃 Maruoka Akira [博士(工学)]
環境都市・建築デザインコース 教授
専門分野
- 構造工学Structural Engineering
- 数値流体力学Computational Fluid Dynamics
写真

研究課題
- 有限要素法による数値流体解析
Computational fluid dynamics based on finite element method - 数値流体解析の風工学に対する適用
Application of computational fluid dynamics to wind engineering problem
[ Key Words: finite element method, computational fluid dynamics, wind engineering ]
研究シーズ
本研究室では、連続性の高い基底関数を用いた数値流体解析手法の開発を行っています
画像の解説
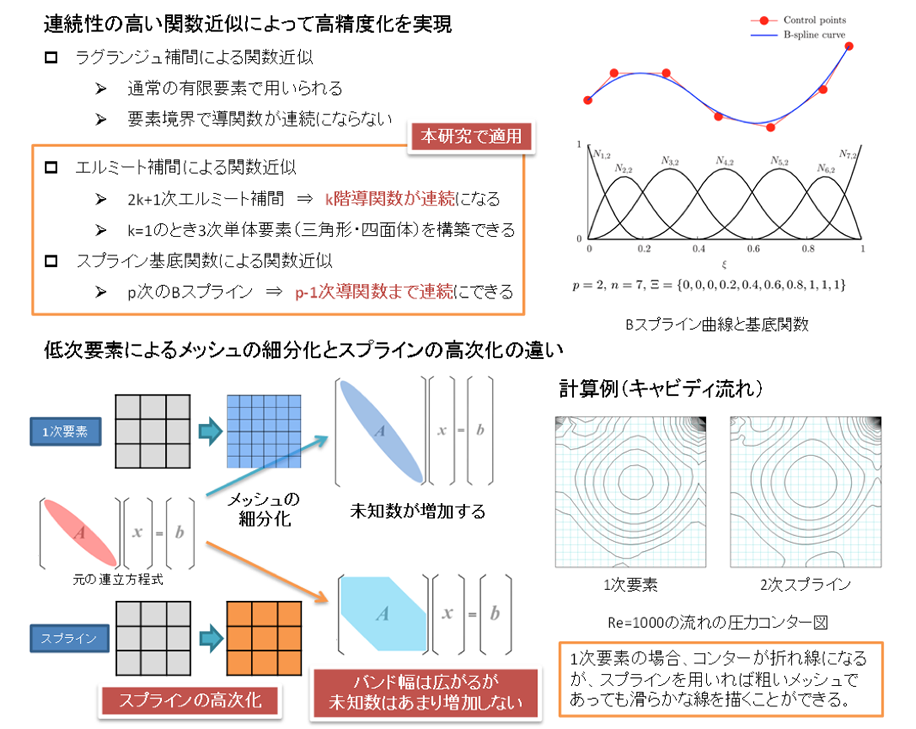
連続性の高い関数近似によって高精度化を実現
ラグランジュ補間による関数近似
通常の有限要素で用いられる
要素境界で導関数が連続にならない
本研究で適用
エルミート補間による関数近似
2k+1次エルミート補間
k階導関数が連続になる
k=1のとき3次単体要素(三角形・四面体)を構築できる
スプライン基底関数による関数近似
p次のBスプライン
p-1次導関数まで連続にできる
低次要素によるメッシュの細分化とスプラインの高次化の違い
スプラインの高次化
バンド幅は広がるが未知数はあまり増加しない
計算例(キャビディ流れ)
1次要素の場合、コンターが折れ線になるが、スプラインを用いれば粗いメッシュであっても滑かな線を描くことができる。
ラグランジュ補間による関数近似
通常の有限要素で用いられる
要素境界で導関数が連続にならない
本研究で適用
エルミート補間による関数近似
2k+1次エルミート補間
k階導関数が連続になる
k=1のとき3次単体要素(三角形・四面体)を構築できる
スプライン基底関数による関数近似
p次のBスプライン
p-1次導関数まで連続にできる
低次要素によるメッシュの細分化とスプラインの高次化の違い
スプラインの高次化
バンド幅は広がるが未知数はあまり増加しない
計算例(キャビディ流れ)
1次要素の場合、コンターが折れ線になるが、スプラインを用いれば粗いメッシュであっても滑かな線を描くことができる。
研究のキーワード
シミュレーション,数値流体力学(CFD),有限要素法,ソフトウェア作成












